MATERI PELAJARAN SEKOLAH : TEORI RELATIVITAS

1. Relativitas Galilean  

Jauh sebelum Einstein lahir, Galileo Galilei telah membuat  pemikiran tentang relativitas atau yang lebih dikenal dengan transformasi relativitas Galilean. Bahkan Isaac Newton pun mengembangkan hukum-hukum tentang gerak dari transformasi galilean ini.

Untuk memahami relativitas galilean  tinjaulah kerangka acuan di bawah ini :  

Ada dua macam obyek dengan kerangka acuannya  masing-masing. Obyek O_A dengan kerangka X_AY_AZ_A dan obyek  O_B dengan kerangka X_BY_BZ_B. O_A melihat O_B bergerak  dengan kecepatan v ke arah sumbu X_B.   Jika merunut pada pemikiran Galileo, karena sumbu Y_A sejajar dengan Y_B dan sumbu Z_A sejajar  pula dengan Z_B, maka bisa dikatakan Y_A = Y_B  dan Z_A = Z_B,  sehingga yang perlu diperhatikan hanyalah sumbu X_A dan  X_B, dengan pengamat A di O_A dan pengamat B di O_B.

Tinjau dua pengamat tersebut, O_A dan O_B yang bergerak relatif satu sama lain dengan kecepatan tetap v.  Kecepatan O_B relatif terhadap O_A adalah v dan kecepatan O_A relatif terhadap O_B adalah − v. Waktu permulaan t = 0 jadi  baik O_A maupun O_B bersamaan waktunya. Perhatikan diagram berikut.

Menurut Galileo,   OA melihat OB bergerak sejauh :  

  XB = XA + vt

Sementara jika dibalik, OB melihat OA bergerak sejauh :  

  XA = XB − vt

Perhatikan bahwa baik di O_A maupun O_B, waktu t  senantiasa bernilai sama. Inilah yang dikenal sebagai  transformasi Galileo .  

Sekarang anggaplah suatu benda ditempatkan pada titik P (lihat gambar 2). Kedua pengamat mendapatkan persamaan kecepatan dan posisi sebagai berikut.

XB = XA + vt

YA = YB

vBx = vAx + v

vAy = vBy

Dimana X_A dan Y_A adalah koordinat titik P diukur oleh pegamat A dan X_B dan Y_B adalah koordinat yang diukur oleh pengamat B. Sedangkan v_Ax, dan v_Ay adalah komponen kecepatan P yang diukur oleh A, dan v_Bx dan v_By adalah komponen kecepatan yang diukur oleh B. Waktu tang diukur t dan v adalah kecepatan relatif kedua pengamat. Persamaan posisi dan kecepatan ditulis dalam bentuk vektor adalah sebagai berikut. Persamaan yang muncul dikenal dengan Transformasi Relativitas Galilean.

rB = rA + v t

vB = vA + v

Semua perubahan bentuk persamaan ini  dapat dilihat pada diagram berikut:

Dengan demikian galileo berkonsep bahwa tidak ada ruang mutlak yang ada adalah ruang relatif. Isaac Newton dengan mengacu pada transformasi Galileo,  juga menolak adanya ruang mutlak. Menurut Newton, sebuah  obyek hanya bisa disebut bergerak jika telah terjadi  perubahan jarak dengan obyek lain (sembarang obyek) di  dunia ini. Jadi yang ada hanya ruang relatif. Namun baik Galileo maupun  Newton tetap meyakini adanya waktu mutlak. Yakni waktu  bagi seluruh obyek di alam semesta ini adalah identik,  tanpa dipengaruhi kedudukan dan kecepatan setiap  obyek. Anggapan tentang waktu mutlak inilah yang  direvisi oleh Einstein dengan relativitas khususnya.  

2. Teori Relativitas Khusus

Gelombang tali, gelombang bunyi, gelombang permukaan air dan gelombang mekanik lainnya merambat memerlukan medium. Cahaya atau gelombang elektromagnetik lainnya dapat merambat melalui ruang hampa. Pada abad XIX, digunakan suatu hipotesa tentang eter sebagai medium perambatan gelombang elektromagnetik, disebut teori Huygens.

Hipotesanya sebagai berikut : Alam semesta di jagad raya ini banyak dipenuhi eter yang tidak mempunyai wujud tetapi dapat menghantarkan perambatan gelombang.

Teori gelombang Huygens telah membuat masalah yang harus memperoleh penyelesaian, yakni tentang medium yang merambatkan cahaya yang disebut eter.

Pada tahun 1887 Michelson dan Morley mengadakan percobaan-percobaan yang sangat cermat, hasilnya sangat mengejutkan, karena adanya eter tidak dapat dibuktikan dengan percobaan. Michelson dan Morley, dua orang sarjana fisika berkebangsaan Amerika Serikat, mencoba membuktikan keberadaan eter tersebut. Alat yang digunakan dinamakan Interferometer.

Ternyata hasil percobaan Michelson dan Morley menunjukkan kesimpulan bahwa hipotesis adanya eter yang terdapat di setiap tempat adalah salah, atau tegasnya eter tidak ada.

Hasil percobaan Michelson dan Morley mencakup dua hal yang penting.

Hipotesa tentang medium eter tidak dapat diterima sebagai teori yang benar, sebab medium eter tidak lulus dari ujian pengamatan.

1. Kecepatan cahaya adalah sama dalam segala arah, tidak bergantung kepada gerak bumi.

Pada tahun 1905 Einstein mengemukakan Teori Relativitas Khusus dengan dua postulat yang menjadi dasar pengembangan Teori Relativitas Umum. Dua postulat tersebut adalah bahwa sifat semesta (universe) pengamat tidak berubah jika kondisi inersia pengamat berubah serta kecepatan cahaya dalam vakum adalah sama di semua pengamat.

Contoh eksperimen pemikiran dari Teori Relativitas Khusus adalah Paradoks Kembar, jika A dan B yang kembar, A diam di bumi dan B keluar dari bumi dengan kecepatan mendekati cahaya maka saat B kembali ke bumi akan berumur lebih muda daripada A.

Dalam kasus di lapangan prediksi pemikiran ini terjadi pada jam pesawat supersonik yang menjadi tidak sinkron dengan jam di bumi setelah melakukan perjalanan.

Postulat Einstein tentang Teori Relativitas Khusus (Postulat = kesimpulan, diatas hipotesa dibawah teori ), hanya menjelaskan benda bergerak dengan ν  c dengan kecepatan tetap (GLB)

Postulat I

Hukum-hukum fisik dapat dinyatakan dengan persamaan yang berbentuk sama, dalam semua kerangka acuan yang bergerak dengan kecepatan tetap satu terhadap yang lain, artinya bentuk persamaan dalam fisika selalu tetap meskipun diamati dari keadaan yang bergerak.

Postulat II

Kelajuan cahaya dalam ruang hampa sama besar untuk semua pengamat, tidak tergantung dari gerak pengamat. Artinya laju cahaya tetap c = 3 10⁸ m/s walaupun diamati oleh pengamat yang diam maupun oleh pengamat yang sedang bergerak, dan tidak ada benda yang kelajuannya = laju cahaya.

1. Asas Relativitas Einstein

Telah dibahas bahwa kecepatan cahaya ke segala arah adalah sama, tidak bergantung pada gerak bumi. Tetapi bumi bukanlah satu-satunya planet yang ada dalam jagad raya ini. Kalau begitu bagaimana kecepatan cahaya itu ditinjau dari planet lain yang geraknya berbeda dengan gerakan bumi.

Pada tahun 1905, Einstein mengusulkan bahwa kecepatan cahaya yang besarnya sama ke segala arah itu berlaku ditempat-tempat lain dalam alam semesta ini. Tegasnya kecepatan cahaya adalah sama, tidak bergantung kepada gerak sumber cahaya maupun pengamatnya.

Teori Einstein membawa akibat-akibat yang sangat luas dirasakan agak menyimpang dari pengalaman-pengalaman yang kita peroleh sehari-hari.

1. Relativitas penjumlahan kecepatan.

Bila v₁ adalah laju kereta api (benda ke 1) terhadap tanah/bumi, dan v₂ adalah laju orang (benda ke 2) terhadap kereta api, maka laju orang terhadap tanah/bumi :

v1 = laju benda ke 1 terhadap bumi
v2 = laju benda ke 2 terhadap benda ke 1
v = laju benda ke 2 terhadap bumi
c = kecepatan cahaya

Kesimpulan:

1.    Kecepatan cahaya (c) dalam segala arah adalah sama tidak tergantung pada gerak pengamat sumber cahaya

2.    Dalam penyelesaian soal, arah kecepatan benda (v) adalah positif jika benda bergerak mendekati pengamat, begitu juga sebaliknya

2. Dilatasi waktu (Pemuaian waktu)

Pengertian dilatasi waktu ialah selang waktu yang dipengaruhi oleh gerak relatif kerangka (v). selang waktu yang diamati oleh pengamat yang diam (t_o) dengan selang waktu yang diamati oleh pengamat yang bergerak dengan kecepatan v adalah berbeda.

Hubungannya dimana Δt adalah waktu yang tercatat menurut pengamatan pengamat yang bergerak dengan kecepatan v

Δt  =

Δto = selang waktu yang diamati pada kerangka diam (diukur dari kerangka bergerak)

Δt = selang waktu pada kerangka bergerak (diukur dari kerangka diam)

Kesimpulan:
Semakin cepat suatu benda bergerak maka semakin besar selang waktu yang dialami benda tersebut.

Contoh Soal:

1. Dua orang A dan B adalah anak kembar. Pada umur 20 tahun A pergi ke ruang angkasa dengan pesawat yang lajunya 0,8 c dan kembali ke bumi pada saat B berumur 30 tahun. Berapakah umur B menurut A yang baru kembali?

Jawab:

A bergerak bersama pesawat dengan v = 0,8 c sehingga A sebagai kerangka yang diam, maka pertambahan umur yang ingin dihitung A adalah Δt_o . Menurut B sebagai kerangka yang bergerak terhadap pesawat, selang waktu Δt = 30 − 20 = 10 tahun

Δt  =

10 =

10 =

10 =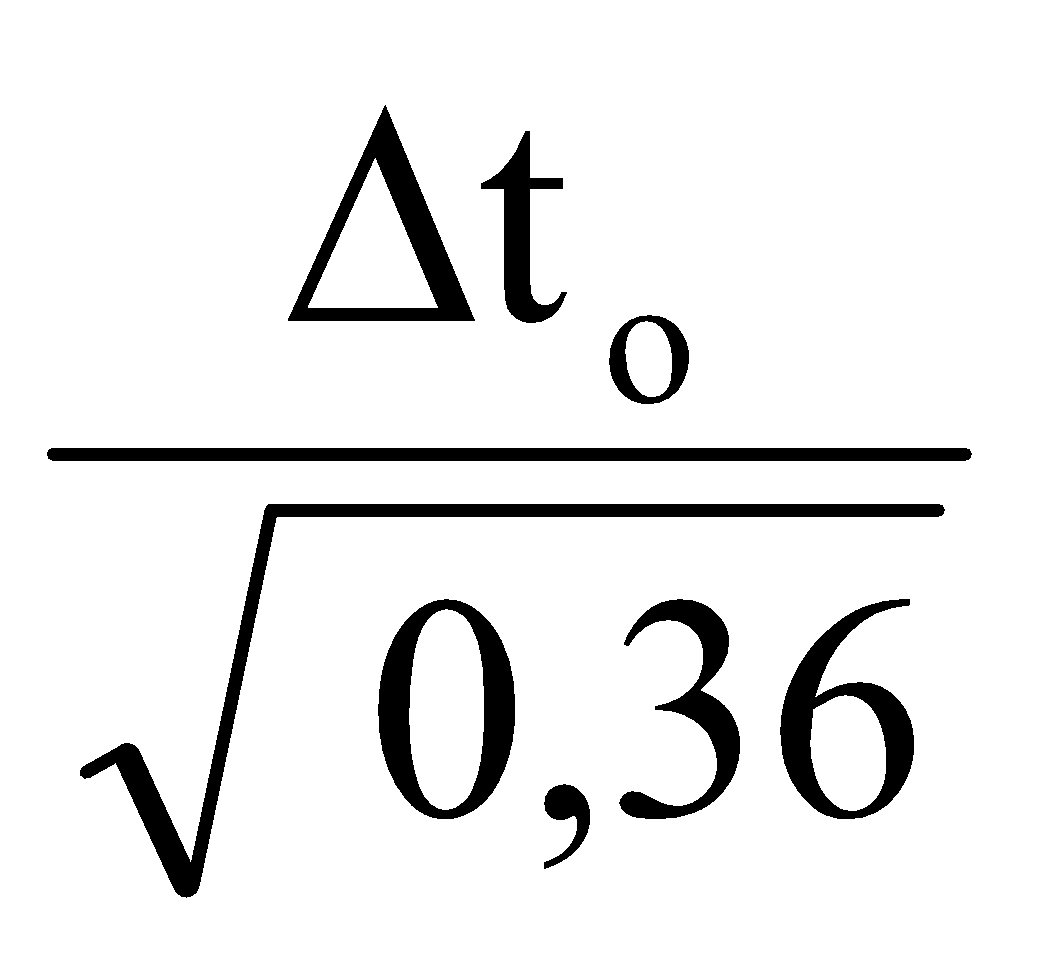

10 =

Δto = 6 tahun

Jadi menurut A, umur B seharusnya bertambah 6 tahun (Δt_o), bukan 10 tahun (Δt) dan menurut A umurnya baru  20 + 6 = 26 tahun

C. Kontraksi Lorentz. (pemendekan Lorentz)

Benda yang panjangnya L_o, oleh pengamat yang bergerak sejajar dengan panjang benda dan dengan kecepatan v, panjangnya akan teramati sebagai L.

L = panjang benda pada kerangka bergerak
Lo = panjang benda pada kerangka diam

Kesimpulan :

Benda yang bergerak dengan kecepatan mendekati kecepatan cahaya akan tampak lebih pendek (berkontraksi) bila diukur dari kerangka diam.

4. Massa dan Energi Relativistik

Massa benda yang teramati oleh pengamat yang tidak bergerak terhadap benda, berbeda dengan massa yang teramati oleh pengamat yang bergerak dengan kecepatan v terhadap benda.

m_o = massa diam atau massa yang teramati oleh pengamat yang tidak bergerak terhadap benda.

m = massa relativistik = massa benda dalam kerangka bergerak atau massa yang teramati oleh pengamat yang bergerak dengan kecepatan v terhadap tanah

Kesimpulan :

Massa (sifat kelembaman) suatu benda akan bertambah besar dengan makin besarnya kecepatan.

Perhatikan kurva berikut ini.

Di dalam mekanika yang disempurnakan, lazimnya disebut mekanika relativistik, energi benda yang kecepatannya v dan massanya m_o (dalam keadaan diam), bukan mo.v2, melainkan :

Ek = moc2

Ek = − mo c2

Besaran energi kinetik menunjukkan dua besaran, yaitu :

dan mo c2

Einstein menginterpretasikan bahwa sebagai energi total (E) benda yang bermassa m dengan kecepatan v, sedangkan m_o c² energi total ketika diam (E_o).

Jadi : = m c2 + Ek

Atau E = Eo + Ek

Ek = E − Eo

Ek = m c2 − mo c2

Ek = (m - mo) c²

E = energi total = m c²
Eo = energi diam = mo c²
Ek = energi kinetik benda

Akibat interpretasi ini, benda yang bermassa m memiliki energi sebesar :        E = mc². Dengan perkataan lain massa setara dengan energi.

 Semakin cepat suatu benda bergerak maka semakin besar energi total (E) yang dimiliki benda, karena massa relativistiknya bertambah besar.

Catatan:

Pada pembahasan relativitas tidak berlaku hukum kekekalan massa karena massa benda yang bergerak > massa benda diam, tapi hukum kekekalan energi tetap berlaku

Contoh Soal:

1. Sebuah elektron yang mempunyai massa diam m_o bergerak dengan kecepatan 0,6 c. Hitunglah energi kinetik elektron tersebut ?

Jawab:

Karena elektron bergerak dengan v = 0,6 c maka massa relativistiknya adalah: 

m =

Energi kinetik elektron:

Ek = (m - mo) c²

= [ - mo] c²

= [ - 1] mo c²

= [ - 1] mo c²

= mo c²

= 0,25  mo c²

= 0,25  Eo

Jadi energi kinetik elektron yang bergerak = 0,25 kali energi diamnya.

3. Teori Relativitas Umum

Pada tahun 1915 Albert Einstein mempublikasikan sebuah teori yang kemudian disebut Teori Relativitas Umum oleh Akademi Sains Prussia. Teori-teori Einstein merupakan hal baru dalam dunia fisika saat itu dan beberapa bagian menyanggah teori Newton.

 Teori Relativitas Umum menggambarkan alam semesta sebagai hubungan antara materi dan geometri ruang-waktu (spacetime). John Wheler menyederhanakan Teori Relativitas Umum Einstein ini dalam satu kalimat: materi membuat ruang-waktu melengkung (curved), dan ruang-waktu membuat materi bergerak (motion). Kombinasi geometri-materi inilah yang kita rasakan sebagai gravitasi. Teori Relativitas Umum menjelaskan interaksi pada skala makro atau tingkat kasat mata, misalnya peredaran planet, bintang, dan galaksi

 Konsep relativitas khusus memandang ruang-waktu  sebagai jalinan koordinat mirip sehelai permadani yang  dibentangkan di lantai, alias datar. Dua tahun  kemudian, Eisntein tidak bisa mempertahankan anggapan  ruang-waktu yang datar ini ketika ia mencoba  menerapkan kaitan antara relativitas khusus dan  gravitasi. Akhirnya setelah memainkan matematika yang cukup rumit dan dengan  menganggap bahwa cahaya adalah partikel yang  sebenar-benarnya (foton) hingga bisa dipengaruhi gravitasi,  didapatkanlah relativitas umum, yang dirumuskan  Einstein di tahun 1916 dan demikian menggemparkan.  Pada intinya, ketika di ruang-waktu terdapat obyek  yang cukup masif atau padat (seperti planet, bintang-bintang dan  galaksi), ruang-waktu akan melengkung (mirip mangkok)  dan itulah yang disebut gravitasi. Pada masa kini,  selain mekanika kuantum, relativitas umum adalah  permata nya fisika, yang sanggup menjelaskan  perilaku alam semesta dalam struktur berskala besar.  Penemuan black hole yaitu bintang bergravitasi sangat besar hingga mampu menyerap seluruh cahayanya sendiri terkait erat dengan teori gravitasi Einstein ini.

Gambar7.  Konsep Ruang-waktu dalam Teori Relativitas Umum. Massa mempengaruhi bentuk kontur dimensi ruang-waktu, dan bentuk kotur dimensi ruang-waktu mempengaruhi massa untuk bergerak

Teori Relativitas Umum membuat geger karena menyanggah Persamaan Gravitasi Hukum Newton bahwa gravitasi bukanlah sebuah gaya namun hanya konsekuensi dari akibat pelengkungan ruang-waktu. Waktu menjadi parameter bersama ruang tiga dimensi membentuk ruang-waktu atau spacetime, ruang-waktu memiliki referensi terhadap kejadian (event) yang secara matematis disimbolkan dengan koordinat (t, x, y, z) atau dalam koordinat angular (t, r, θ, dan φ).

Teori Relativitas Umum tidak dibahas lebih jauh dalam buku ini. Melihat riwayat teori ini saja, merujuk pada kata-kata Sir Arthur Eddington di tahun  1930 an, pada saat itu hanya ada 3 orang  di dunia yang bisa memahami relativitas umum, yakni  Einstein dan Eddington sendiri, serta orang muda India  yang saat itu sedang berlayar ke Inggris untuk  menuntut ilmu di Cambridge Inggris di bawah asuhan Eddington bernama  Subrahmanyan Chandrasekhar.  
Rangkuman

1. Persamaan yang  dikenal dengan Transformasi Relativitas Galilean. 

rB = rA + v t

vB = vA + v

2. Teori relativitas khusus didasarkan pada dua postulat, yaitu:

• Postulat I

Hukum-hukum fisika berlaku pada suatu kerangka koordinat S, berlaku juga bagi kerangka koordinat yang lain (S'), yang bergerak dengan kecepatan tetap relatif terhadap S. 

• Postulat II

Nilai cepat rambat cahaya di ruang hampa adalah mutlak/sama, tidak tergantung pada gerak pengamat maupun sumber cahaya

3.                  Relativitas penjumlahan kecepatan.

v1 = laju benda ke 1 terhadap bumi
v2 = laju benda ke 2 terhadap benda ke 1
v = laju benda ke 2 terhadap bumi

4. Dilatasi waktu (Pemuaian waktu)

Δt  =

Δto = selang waktu yang diamati pada kerangka diam (diukur dari kerangka bergerak)

Δt = selang waktu pada kerangka bergerak (diukur dari kerangka diam)

5. Kontraksi Lorentz. (pemendekan Lorentz)
   Benda yang panjangnya L_o, oleh pengamat yang bergerak sejajar dengan panjang benda dan dengan kecepatan v, panjangnya akan teramati sebagai L.

L = panjang benda pada kerangka bergerak
Lo = panjang benda pada kerangka diam

6. Massa dan Energi Relativistik

Massa benda yang teramati oleh pengamat yang tidak bergerak terhadap benda, berbeda dengan massa yang teramati oleh pengamat yang bergerak dengan kecepatan v terhadap benda.

m_o = massa diam atau massa yang teramati oleh pengamat yang tidak bergerak terhadap benda.

m = massa relativistik = massa benda dalam kerangka bergerak atau massa yang teramati oleh pengamat yang bergerak dengan kecepatan v terhadap tanah

Besaran energi kinetik 

Ek = − mo c2

Ek = m c2 − mo c2

Ek = (m - mo) c²

Ek = E − Eo

E = energi total = m c²
Eo = energi diam = mo c²
Ek = energi kinetik benda

7. Teori Relativitas
   

   Umum menggambarkan alam semesta sebagai hubungan antara materi dan geometri ruang-waktu (spacetime). Waktu menjadi parameter bersama ruang tiga dimensi membentuk ruang-waktu atau spacetime, ruang-waktu memiliki referensi terhadap kejadian (event) yang secara matematis disimbolkan dengan koordinat (t, x, y, z) atau dalam koordinat angular (t, r, θ, dan φ).